Challenge Source

p = random_prime(2**1024)
q = random_prime(2**1024)
a = randint(0, 2**1024)
b = randint(0, 2**1024)

def read_flag(file='flag.txt'):
    with open(file, 'rb') as fin:
        flag = fin.read()
    return flag

def pad_flag(flag, bits=1024):
    pad = os.urandom(bits//8 - len(flag))
    return int.from_bytes(flag + pad, "big")

def generate_keys(p, q):
    n = p * q
    e = 0x10001
    return n, e

def encrypt_message(m, e, n):
    return pow(m, e, n)

flag = read_flag()
m = pad_flag(flag)

n, e = generate_keys(p, q)
assert m < n

c = encrypt_message(m, e, n)

print(c)
print(n)
print(p + b^2 * q)
print(a^2 * p + q)

Idea

Well, this is just classic RSA encryption. On its own, this scheme is definitely not breakable. However, the author provides some additional values $h_0, h_1$ so that somehow, we can use them to decrypt the encrypted value $c$:

where $a$, $b$ is some random value $\in [0, 2^{1024})$.

My teammate immediately recognized (god 😢) that:

For which you can reason it by doing the following calculations:

Let's set $\frac{b}{a}\frac{q}{p} + \frac{a}{b}\frac{p}{q}$ to be $k$.

If $k$ is small enough to $a$ and $b$, we can approximate it to be

Since $\frac{q}{p}, \frac{b}{a}$ and their reciprocals involve in the sum making up $k$, the bigness of $k$ depends on $\frac{max(p, q)}{min(p, q)}$ and $\frac{max(a, b)}{min(a, b)}$. And you can reason that for any two numbers $x, y$ generated at random in the same interval, the ratio $\frac{max(x, y)}{min(x, y)}$ is expected to be small.

During local test, I realized that $k$ is very small (like, $2$ or $3$ or something...). In fact, let's plot $k$ for different values of $p, q, a, b$ and see how it goes 🙂

Probability density graph of k.

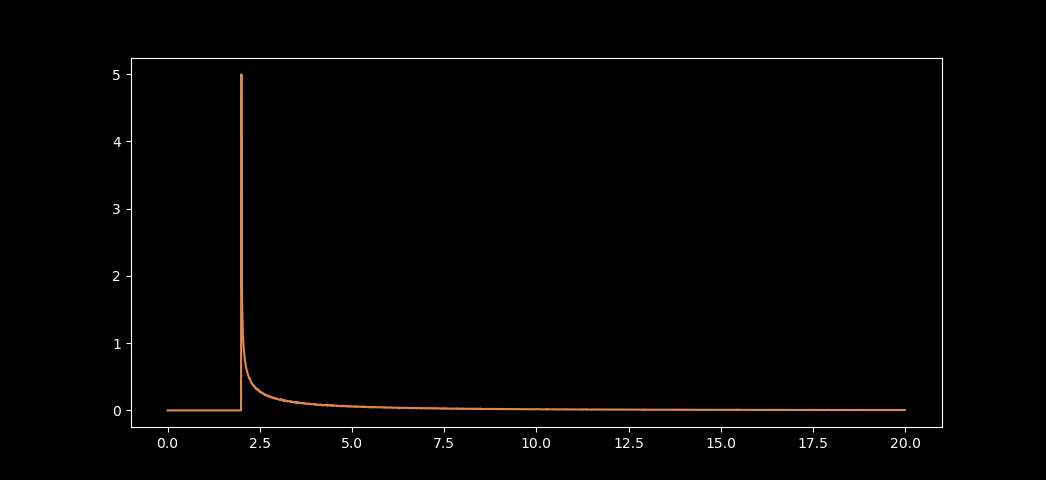
The left column represents the percentage of occurances for a certain $k$. And you can see for ALMOST ALL cases, $k$ will just land around on some value $\le 6$. (yes, while you can argue that the spike of $2$ is just 5%, so the rest could be much bigger, however, the probability of $k$ landing $> 20$ is just 12%)

Also, you can notice that the plot is flat before a sudden spike around $k = 2$. This happens because $k$ can be represented in the form of $\frac{1}{x} + x$, and from AM-GM Inequality, $\frac{1}{x} + x \ge 2\sqrt{\frac{1}{x}x} = 2$ for any $x > 0$.

Anyways, this means in most cases, we can expect:

or if you are really skeptical, you can bound it to be $\le ab + 10000$, just to be sure 🙂 This means that we can find $ab$ just by bruteforcing 10000 values around $\sqrt{\frac{h_0h_1}{n}}$.

Get $p$

Knowing $ab$, we now have 4 equations with 4 variables to solve:

for which we can lend the power of magic Sagemath to solve for $p,q$.

from sage.all import *
from tqdm import trange

c = 8572900207835762766259060305548427890100883047397634495461699978853157157614537323169347948562539226943681557963690343113654640872734234635812404134737383783029729221882136594985076147296741783975976308542646646810930077508306094278881958489094577466122474005274780847502484006774122175180575134906406965261990134809789771668692230279546111615898299677351494730026393299745116126441043262641839846131458109835024756668882646302817842268403187061058095410531259459671076936340425779509762997737719853997033122063887141701633633320429028875760558509090378244944304521100714575766987495025277855338621083017737516612418
n = 11144809766924753211164169820974462795856999866851443978190116700121363041989551071283939406281584000345497130693285334786351068731714844065338178589052164965325272282738320690462179192218231489414187602007189279178640751309024526964298676986141201862905207755202946987885824563821850086298674083250354794989520315263319887676335677763156987501376451785566994901716198026893601133060745072362354091538721508265964958576574770694885291955086273571799403020416375990066994984333344295830201448319348356984141129557424755917133168216662244421360263592451413336939492881342257615928593787731918025125347411493314907250137
h0 = 3133548371772245794593916200216569789009977503838749561227383433777720559941789482302916747603629163277628624218728934067099751860342707727093284736792795911695291350493714661780427322085098620600442730601203727048863482544984150704785568558089024822242137835533188983145916911039381864946181510766072421365244229323632933214703949194559838270346065808390788292338719229269524606818971098272185892178470535466837645119304408225231332458404102608745644737712878232270144653748091436259421085576899894410825994764509434190271250735054775427479336540747164022736063724088385024013450114201117597406901351692873529770371805217775170905068961082711810613758277323468498024046033975544974993657043847859384646871490664090364968788225608324873580922409806934637562732699242491794243842510137720412106011270126856983601691379316962610115528724097947971496018172633530779698135626404996346034214279586492856257103552654185991624401974
h1 = 1668414440918184768102355070614199463515793278471647551081913918452877485930426726226888602387669498229921420169090265893271687426728329309931304042833872472475849661618647319286811295064264833639171767419811286840565958014252378459070198913214095511167368116072393143874905742547670514329775410132929858061858466466966832673233837546616958733459536386756690536101619509572857744943940172226354331174483476689882385303341939713713582201065151215959817799687574284712464653518663899972395427884233952547367314997783361776439415679136448860553029913121320416809081351610252174264463832509457873454643897905542501703122708259182482820112852708896076939481486564165447979041966168147292062612542988326875351534914932148857901377696892000822979439668349934754312002375192855438370671607139791178130484207096854031824894563191176002437196868004348552012031601430061559392941224723263095744921218764294325481602675909958988713011638

P = PolynomialRing(QQ, names=('b', 'q'))
b, q = P.gens()

ab_approx = Integer(isqrt(Integer(h0*h1) / Integer(n)))
for delta in trange(0, 1000):
    ab = ab_approx - delta

    # Here, I substitude a*b = ab and p*q = n 
    # to reduce number of equations & vars
    eqs = [
        n + b**2 * q*q - h0*q,
        ab**2 * n + q*q * b**2 - h1 * b**2 * q
    ] 

    # Copied from somebody's Coppersmith multivariate solver :v
    H = Sequence(eqs, P)
    I = H.ideal()
    if I.dimension() == -1:
        H.pop()
    elif I.dimension() == 0:
        for root in I.variety(ring=ZZ):
            print(root)

# q = 109813633407350440684752357104087423730270808390261227637462376676953120335377705330415425210793126533507813859480119893163026376723863463313335381388502153679899248105338398482841127131263152039296390164162491463575378945424202721526857339615769738614581032689687091169497613753054146273393581209744585087263

Get Flag

Since we have $p,q$, we can now recover the private exponent and solve for flag 🙂

from Crypto.Util.number import *

c = 8572900207835762766259060305548427890100883047397634495461699978853157157614537323169347948562539226943681557963690343113654640872734234635812404134737383783029729221882136594985076147296741783975976308542646646810930077508306094278881958489094577466122474005274780847502484006774122175180575134906406965261990134809789771668692230279546111615898299677351494730026393299745116126441043262641839846131458109835024756668882646302817842268403187061058095410531259459671076936340425779509762997737719853997033122063887141701633633320429028875760558509090378244944304521100714575766987495025277855338621083017737516612418
n = 11144809766924753211164169820974462795856999866851443978190116700121363041989551071283939406281584000345497130693285334786351068731714844065338178589052164965325272282738320690462179192218231489414187602007189279178640751309024526964298676986141201862905207755202946987885824563821850086298674083250354794989520315263319887676335677763156987501376451785566994901716198026893601133060745072362354091538721508265964958576574770694885291955086273571799403020416375990066994984333344295830201448319348356984141129557424755917133168216662244421360263592451413336939492881342257615928593787731918025125347411493314907250137
h0 = 3133548371772245794593916200216569789009977503838749561227383433777720559941789482302916747603629163277628624218728934067099751860342707727093284736792795911695291350493714661780427322085098620600442730601203727048863482544984150704785568558089024822242137835533188983145916911039381864946181510766072421365244229323632933214703949194559838270346065808390788292338719229269524606818971098272185892178470535466837645119304408225231332458404102608745644737712878232270144653748091436259421085576899894410825994764509434190271250735054775427479336540747164022736063724088385024013450114201117597406901351692873529770371805217775170905068961082711810613758277323468498024046033975544974993657043847859384646871490664090364968788225608324873580922409806934637562732699242491794243842510137720412106011270126856983601691379316962610115528724097947971496018172633530779698135626404996346034214279586492856257103552654185991624401974
h1 = 1668414440918184768102355070614199463515793278471647551081913918452877485930426726226888602387669498229921420169090265893271687426728329309931304042833872472475849661618647319286811295064264833639171767419811286840565958014252378459070198913214095511167368116072393143874905742547670514329775410132929858061858466466966832673233837546616958733459536386756690536101619509572857744943940172226354331174483476689882385303341939713713582201065151215959817799687574284712464653518663899972395427884233952547367314997783361776439415679136448860553029913121320416809081351610252174264463832509457873454643897905542501703122708259182482820112852708896076939481486564165447979041966168147292062612542988326875351534914932148857901377696892000822979439668349934754312002375192855438370671607139791178130484207096854031824894563191176002437196868004348552012031601430061559392941224723263095744921218764294325481602675909958988713011638

e = 65537
q = 109813633407350440684752357104087423730270808390261227637462376676953120335377705330415425210793126533507813859480119893163026376723863463313335381388502153679899248105338398482841127131263152039296390164162491463575378945424202721526857339615769738614581032689687091169497613753054146273393581209744585087263
p = n // q
d = pow(e, -1, (p-1)*(q-1))
print(long_to_bytes(pow(c, d, n)))

# b"midnight{1_kN0w_3n0ugh_4b0ut_RSA}\n\xa9\xbd\xd17\xec'\xed\x9c\x19RD\x8f\x9c8\xe4\xb9\x11\xf3\xb5/\xdeC\xff\xe5c\x89_3\xd7F\x1f^\x12 +A\xc3\xc7\\HC\xd9!\xd6`\x86\xa8B\xc0A)4q\x85x<\xbd\xe7@\xa9\xa3\x08\xc2\xb0\xdf\x03\xb9\xbd.\x8f\xa3\xe5\xd8\x8b\xf0\xadw7\xb7\xe1\xa2j\x95\xd9\xe5!\xee\xf2u\xf32\xf1V\x1c"