For a while now, after the death postponed activities of u0K++, I've got a chance to join in idek team (thanks lanleft so much because I'm incredibly socially awkward...). I really like the guys there, they are so vibrant, fun and incredibly smart. I'm not any of those descriptions though, and so, in this CTF, I sliently watch them carry 😗

Challenge

This challenge provides a some sort of Diffle-Hellman key exchange-ish- protocol in the form of 64x64 matrices in ZZ. The premise is very straight-forward. You're given:

• A matrix Q = B * B.tranpose(), B unknown and random.
• 2 matrices M1, M2 generated from Q and unknown matrices U1, U2:

M1 = U1.transpose() * Q * U1
M2 = U2.transpose() * Q * U2

The challenge has 2 matrices S1, S2 that act as the shared secrets to this protocol.

# Yeah, these 2 things are the same :3
S1 = U1.transpose() * M2 * U1
S2 = U2.transpose() * M1 * U2

It seems like the challenge would be impossible if the matrices U1, U2 are any arbitary matrices, so a condition is added for their generation:

N = 64

def find_poly():
    while True:
        n = random.randint(2, N - 1)
        d = gcd(N, n)
        m = n // d
        if m > 1 and not is_prime_power(m):
            return cyclotomic_polynomial(n)


def circulant_gen():
    h = 1
    R = QuotientRing(ZZ[x], x^N - 1)
    for i in range(100):
        f = find_poly()
        h = R(f * h)
    v = h.list()
    l = N - len(v)
    for i in range(l):
        v.append(0)
    M = matrix.circulant(v)
    return M

# key exchange
U1 = circulant_gen()
U2 = circulant_gen()

Anyways, the goal is to recover flag from its encrypted enc value, which is created like this:

ss = hashlib.sha256(str(S1).encode()).digest()
enc = bytes([x^^y for x, y in zip(FLAG, ss)])
print(enc.hex())

Analysis

This challenge has my brain go buckeroo 😵‍💫, because I don't know what to focus on. At first, I thought the polynomials used to create the matrices Ux has something important to do with all of this, but all of that just go to nowhere. My teammate A~Z had an idea of using QuadraticForm do something with the factorization of matrices, but I had no idea what that is (and still doesn't). After a while, he also abandoned that idea as well and realized the actual solution thanks to the suggestion of 蛋捲鯛魚燒.

From here, let's just refer to matrices M1, M2 as $M$ and U1 and U2 as $U$.

In the end, it turns out everything just tie into the fact that $U$ matrices are circulant. For more details, you can visit this link. But for a recap, a circulant matrix is an nxn matrix that has this form:

The circulant matrix has a bunch of properties, one of them is $AB = BA$ which allows this protocol to work (S1 == S2). However, 蛋捲鯛魚燒 realized that it has a very special property:

Indeed, it turns out EVERY CIRCULANT MATRIX has the same set of (normalized) eigenvectors! Which means that given a circulant matrix $U$, it doesn't matter what $U$ is, as long as it's circulant, we can know $P$ in $U$'s diagonalization form $U = PDP^{-1}$. Quote Wikipedia:

However, we still doesn't know what $D$ is in this case. But here's the cool stuff: We can find $D$ through $M$ and $Q$. Let's write $M$ in terms of $P$ and $D$:

What's great about this is that you can multiply $P^T$ to the left of $M$ and $P$ to the right of $M$ and you can see some sort of symmetry:

Let $f(M) = P^T M P$ and now we have:

Because $D$ is a diagonal matrix, A~Z has a very interesting insight:

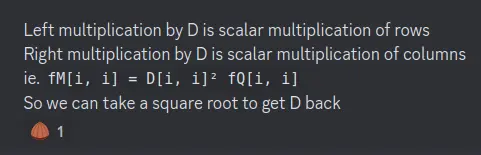
After we get $D$, we find $U = PDP^{-1}$, which then we can compute S1 -> ss -> solve flag!!!

Solve Script

from sage.all import *
from ast import literal_eval
import hashlib

# EVERY nxn circulant matrices has a fixed
# set of eigenvectors, which can be computed very
# easily based on the roots of unity.
# https://www.wikiwand.com/en/Circulant_matrix
N = 64
C = ComplexField(4096)
w = exp(2 * C(pi) * C(i) / N)

# Read outputs from file.
lines = open("output.txt", "r").readlines()
Q  = Matrix(ZZ, N, N, literal_eval(lines[0]))
M1 = Matrix(ZZ, N, N, literal_eval(lines[1]))
M2 = Matrix(ZZ, N, N, literal_eval(lines[2]))
enc = bytes.fromhex(lines[3].strip())

# This allows us to diagonalize circulant
# matrices very easily.
# ( Let U1 = P D1 P^-1, U2 = P D2 P^-1 )
P = [[w**(i*j) for i in range(N)] for j in range(N)]
P = Matrix(C, P)

# But we don't want to diagonalize it, 
# instead, we take advantage of this property:
#    U   = P D P^-1 
# => U.T = P^-1.T D.T P.T 
#        = P^-1.T D P.T      (since D.T == D)

# Let f(M) = P.T * M * P
#  => f(M) = D * f(Q) * D
fQ  = P.T * Q  * P
fM1 = P.T * M1 * P
fM2 = P.T * M2 * P

# This means
# f(M)[i, i] = D[i, i]^2 * f(Q)[i, i] 
# => D (or D1, D2) is recoverable.
# => U (or U1, U2) is recoverable.
s1 = sqrt(fM1[0,0] / fQ[0,0])
D1 = [s1]
for i in range(1, N):
    D1.append(fM1[0, i] / (s1*fQ[0, i]))
D1 = matrix.diagonal(C, D1)
U1 = P * D1 * P**-1
U1 = Matrix(ZZ, [[round(col.real()) for col in row] for row in U1])

S1 = U1.T * M2 * U1
ss = hashlib.sha256(str(S1).encode()).digest()
flag = bytes([x^y for x, y in zip(enc, ss)])
print(flag)

The flag is: ptm{1s_7h15_l1n34r_0r_qu4dr4t1c}