Intro

Once in a while, there comes a problem that makes you more conscious about your insignificant intelligence... Today, it comes in the form of a CTF challenge :'<<

Basically, there's this challenge:

• generates a random polynomial $f(x)$ with $N=$ 20000156 terms in $\mathbb{F}_{p}$, where $p=$ 20000159,
• evaluates the outputs $f(0), f(1), ..., f(p-1)$ except for $f(69), f(420)$ and $f(1337)$,
• gives us said outputs,
• gives us the FLAG XORed with the sha512() hash of $f(x)$'s coefficients array.

Trying stuffs...

Since it's hard to crack sha512(), or reverse XOR function with 0 knowleges about one of its inputs, our only route is to recover $f(x)$ from its outputs.

Lagrange Interpolation

So, if you're a noob like me, your first thought will probably be:

"Well, this is a piece of cake.

I'll just use the Lagrange Interpolation. They have this fancy math that computes a polynomial's $N$ coefficients from its $N$ evaluations.

We meet all the requirements needed to carry out the computation."

So you gleefully copy an implementation from the Internet, adding inputs, modify stuffs, typing, thinking to yourself: "EZ".

You run the code and wonder why it takes so long. Maybe the output array is too big and needed some time to load? No, it had already been done! You throw a tqdm bar into the main loop of the code and see that it estimates the algorithm will be running for another 7000 hours.

Shit 💩.

You dig into the implementation of Lagrange Interpolation, and realize that given a polynomial with $N$ terms:

• it computes the sum of $N$ terms,
• each term is the product of smaller $N-1$ linear polynomials.

An $O(N^2)$ runtime...

This algorithm works fast for small polynomial sizes, like 2 or 3 and some numbers close to it like 10000, but not 20000156. This is when you GASP: "This is not Crypto, this is some Codeforces obsure 200+ IQ optimization problem!!" You know you suck, but you still want try solving a coding optimization stuffs anyways, to see where it goes.

The Vandermonde Matrix

From your experiences of watching math videos on Youtube, feeling smart then remember like 1% about it the next day, you realize that you still don't know what to do now and feel like shit (meanwhile, your teammate is saying something about vandermonde) maybe sometimes we need to derail to some random ideas to get to smart one, so that's what you did.

So you definitely did look at this wiki page and did not have an insight on your own:

The evaluation of $f(x) = \sum_{k=0}^{N-1} f_k x^k$ at $x_0$ can be represented as a dot product: $f(x_0) = (x_0^0, x_0^1, ..., x_0^{N-1}) \cdot (f_0, f_1, ..., f_{N-1})$.

Or maybe, as a multiplication of 1xN matrix with another Nx1 matrix:

And you see that you can extend the 1xN matrix on the left so that on the right side you can compute not only $f(x_0)$, but also $f(x_1), f(x_2), ...$ and so on:

The NxN matrix on the left side seems like a special type of matrix. Maybe you discovered a new thing 😱 (and not something already been discovered and called the Vandermonde Matrix)? Anyways, you decide to name this thing the Vandermonde Matrix, because it sounds right somehow...

Let's rewrite the equation into: $V \text{ } \overrightarrow{f} = \overrightarrow{y}$, where:

• $\overrightarrow{f}$ is $f(x)$'s coefficients vector.
• $\overrightarrow{y}$ is $f(x)$'s outputs vector.
• $V$ is the Vandermonde matrix.

Which leads to $\overrightarrow{f} = V^{-1} \text{ } \overrightarrow{y}$. As long as $x_0 \neq x_1 \neq x_2 \neq ... \neq x_{N-1}$, $V$ is invertible. Because we have $\overrightarrow{y}$ and want to find $\overrightarrow{f}$, this shifts our focus into...

A couple of Google searches leads us to this website:

You have a hunch that this route sucks. Matrix multiplication with a vector still takes $O(N^2)$ as far as you know, and at the same time, EggRoll, from your team says this:

Others seem to brush off his idea, and to be honest, they seem tired and confused at that point, so it's understandable. But you remember from the 1% of knowledge you watched in some Youtube video, that FFT is some algorithm that can be done in $O(N\log{N})$, which is something way better than $O(N^2)$, is probably exactly what we need right now!!

Hmm... But you forget what it does...

Fast Fourier Transform

Fast Fourier Transform, or FFT for short, is an algorithm that also can do the convert coefficients -> values thingy. However, this algorithm has a restriction:

The inputs to $f(x)$ must be $\omega_N^0, \omega_N^1, ..., \omega_N^{N-1}$, instead of arbitrary values $x_0, x_1, ..., x_{N-1}$, where $\omega_N$ is any $N$-th root of unity (except 1 to avoid $\omega_N^0 \neq \omega_N^1 \neq ... \neq \omega_N^{N-1}$).

Hmm.. Actually that's what I understand about this...

The actual purpose of FFT seems to be some values -> frequency thingy conversion stuffs. But in this case, it still true (?) idk... math is weird... Maybe I'm wrong on something @.@

But if you want to know the actual definition of FFT, you can read it here: Wiki

To understand why FFT does this, let's formulize things.

Same as before, this relationship between coefficients and values can be represented as the product of a Vandermonde matrix with the coefficient vector $\overrightarrow{f}$:

Let's rewrite the equation into: $D_{\omega_N} \text{ } \overrightarrow{f} = \overrightarrow{y_{\omega_N}}$, where:

• $\overrightarrow{f}$ is $f(x)$'s coefficients vector.
• $\overrightarrow{y_{\omega_N}}$ is $f(x)$'s outputs vector of $f(x)$ evaluated at $\omega_N^0, \omega_N^1, ..., \omega_N^{N-1}$.
• $D_{\omega_N}$ is a special case of Vandermonde matrix, called the DFT matrix, whose entries can be generated solely from $\omega_N$ and their positions.

Same as before, we want to convert values in $\overrightarrow{y}$ -> coefficients $\overrightarrow{f}$, which is esentially the inverse process of FFT.

We have: $\overrightarrow{f} = D_{\omega_N}^{-1} \text{ } \overrightarrow{y_{\omega_N}}$, where $D_{\omega_N}$ is invertible since $\omega_N^0 \neq \omega_N^1 \neq ... \neq \omega_N^{N-1}$. It turns out that the inverse of a DFT matrix is another DFT matrix scaled down by $N$:

Since $\omega_N^{-1}$ is also just another root of unity & multiply with a DFT matrix is just doing FFT, this means that the inverse process of FFT (IFFT) is just another FFT with an extra step of scaling down all the outputs by $N$, which is an $O(N)$ step.

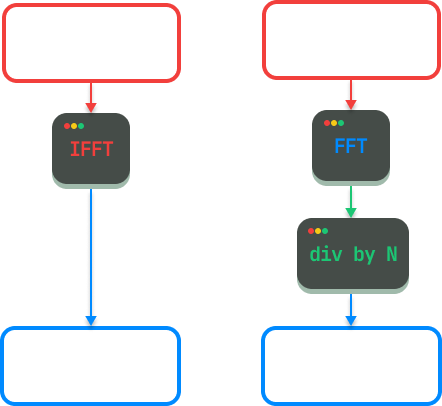
What you can take away from this is that IFFT is as fast as FFT.

If you look at the other methods we found to convert values -> coefficients, the difference it has with the backward process involves an additional process of inverting a really big matrix: A very complex process taking a lot of CPU & RAM. So this seems like a huge hidden win that we just discover blindly :-3

Also, this means that if you can somehow make FFT fast, you can do FFT back-and-forth with ease.

And it turns out there's an optimized version of FFT that has $O(N\log{N})$ runtime, called the Radix-2 FFT! For more details, please consider watching this video by Reducible, this guy is really good :>

So now it seems like we've found our path! However, if you've watched the video like me, you'd notice there are a few problems...

Oh No...

A lot of oh-noes...

Not a Power of 2

In order for this optimized version to work, $N$ must be a power of 2 (that's why this is called "Radix-2 FFT"), and 20000156, well, is not. But we can sort of "cheat" by "pretending" that $f(x)$ has more than 20000156 terms, with the leading coefficients are all $0$s.

So why not, say, think that $f(x)$ has the number of coefficients $N$ = the closet power of two $\geq$ 20000156, idk, like $2^{25}$?

Can't get much more outputs

But then that would mean we need more than 20000156 outputs!! We might want to use Lagrange Interpolation to recover more values. But as we analyzed from the Lagrange Interpolation section, it takes $O(N^2)$ for each input to produce the output!!

Also, in this CTF challenge, we can only get 3 more outputs, because $x \equiv x + 20000159$, so $f(20000160)$ is just $f(1)$... And none of the numbers from 20000156 to 20000159 are powers of 2.

Note from Mistsu in the future:

It turns out, in this particular CTF challenge, we can AND just need to recover $f(69), f(420), f(1337)$, where each calculation takes $O(4*N)$ due to some very clever parameter choices, while still can do FFT in $O(N\log{N})$!

but we're ahead of ourselves at this point heheheh :-)

404 - Root of Unity Not Found

Say, we're able to extend the length of $f$ to $2^{25}$. By then we still wouldn't be able to do IFFT: the algorithm requires a $2^{25}$-th root of unity, and no such thing exists in $\mathbb{F}_{p}$.

Because of number theory and group theory stuffs, any subgroup of the multiplicative group $\mathbb{F}_{p}^{\times}$ must have order dividing $p-1$. This means good luck trying to find $g \not\equiv 1$ such that $g^{x} \equiv 1 \mod {p}$ when $x \nmid p-1$... You can start with 3 to experiment 😘

The only prime factors of $p - 1$ are 2, 10000079, that means $\mathbb{F}_p$ only has 2, 10000079, or 20000158-th roots of unity! But apperantly that means we can only work with cases where $N$ = 2, 10000079 or 20000158!?

Since we can only "pretend" it has more coefficients than 20000156, we're locked to the choice of 20000158. Since 20000158 is not a power of 2, it seems like we can't do FFT in $O(N\log{N})$.

Note from Mistsu in the closer future:

we can :-)

...You might be tempted to extend the current working field to $\mathbb{F}_{p^k}$, where you can find subgroups of $\mathbb{F}_{p^k}^{\times}$ with order dividing $p^k - 1$. However, up until $k = 1000$, $p^k - 1$ is divisible by $2^{13}$ at best. And you might want to stop here, because going further means that your CPU & RAM goes bye bye computing those elements. And you also have to do Larange Interpolation to have outputs of $f$ in that field...

Author's Solution

From this point, I keep exhaust myself until the end of the CTF, trying out ideas, but nothing works. If it works, then the runtime is often $O(pq)$ where $q$ is the biggest prime of $p-1$... And then, the author publish their solution in the Discord Server,

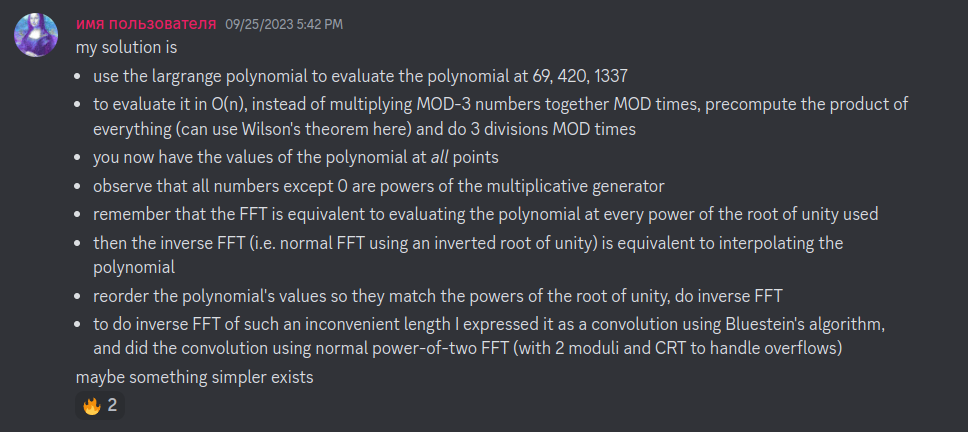
... to which Genni responds:

After reading this, my mind feels even more clueless... So this post should stop here. Part 2 will be focusing on how to understand the solution :v