(flashback)

Me: Hey, I think this challenge uses a faulty version of cosmos/iavl. Cuz you know, like, according to the go.mod file, it uses v0.19.2, which is not the latest version. And then there is this change log of version v0.19.3 saying it prevent sth sth and then there is this blog page posted around that release saying iavl is not good etc etc. I think this is the vulnerability.

L.T.: I think ndh doesn't want to tease our brain too hard, so he wouldn't come up with sth this complex. Let's crack the random function.

Me: I agree. There are so many words and crazy stuffs in this blog so it's probably isn't true.

L.T.: Yeah...

Me: Yeah...

Well, that turns out to be the intended vulnerability of the challenge. But we're not here to discuss that (that blog still hurts my brain btw :'() because we actually figured out a way to crack the random function :happy: (yey)

I've seen the discussion around the challenge and I saw players talking about brute-forcing with multiple cores to get the seed of Go's PRNG. Well, we actually found a way to predict the result without having to find the seed 😗

Although this approach only gives us the correct output $\frac{1}{4}$ of the time, I still think it is interesting so it would be fun to share it 🙂

TL;DR

---

⚠️ (Because I want to write a blog about the details of my discovery, including methods to find it, other methods you can go, what's the challenge is all about, etc, ..., this blog will be a very, probably unnecessarily, lengthy one, and if you're not ready to read it, here is a small recap on what's about to come 🙂)⚠️

(now come to think of it I might have put the whole stream of consciousness in here...)

---

Consider a list of outputs from rand.Intn(n) named $R$ where n is a relatively small number $< 2^{31}$. The $i$-th element $R_i$ will most likely fall into one of these 4 cases:

and we use one of these 4 equations as our strategy to guess the next output. Each round we bet balance/2 (or some number that is linear to balance, like balance/3 or sth, your pick 😙). This strategy allows our money not to run out too quickly when we guess the wrong number while still guarantees our money growing exponentially if we win. Since win amount is $>>$ lose amount, we will benefit in the long run and hence can reach our target balance.

Challenge description

(if you know all the functionalities of the code files, you may skip this section anyways 🙂 )

This challenge is about a Go Application that emulates some sort of online casino stuffs. You interact with the server by sending some JSON data as input, and expect some text data as output.

You can:

• register your username and get $2023$ coin units as your initial balance. The server also restricts you from registering more than 100 accounts or creates another account with an existing username, but it doesn't matter in the context of solving this challenge anyways.

• example request:

{ "recipient": "Casino", "command": "Register", "username": "Orrrrrr" }

• code:

// casino.go
// ...
const MaxPlayers = 100
const InitialBalance = 2023

func (c *Casino) Register(username string) error {
exist, err := c.tree.Has([]byte(username))
if err != nil {
    log.Fatal(err)
}
if exist {
    return errors.New("player-exists")
}
if c.numAccounts >= MaxPlayers {
    return errors.New("max-players")
}
c.numAccounts += 1
c.setBalance(username, big.NewInt(InitialBalance))
fmt.Printf("Added user: %s.\n", username)
return nil
}
// ...

• bet a number n between $[0, 2023)$ with some non-negative amount (if you put in a negative number, the server will correct it to become positive anyways 🤧 -- this became the exploit point of the first challenge, Casino 1, because it didn't check whether the amount is negative or not.)

  The server also generates a number n between $[0, 2023)$. If your n $\neq$ server's n, you will lose :<, else you will win :>

  • when you lose, you lose amount and you will have balance - amount coin units left.
  • when you win, you gain $2022$ * amount.

  Also, the server will tell you what n they generated. ( <- This will become important later on )

• example request:

{ "recipient": "Casino", "command": "Bet", "username": "Orrrrrr", "amount": 123, "n": 456 }

• code:

// casino.go
// ...
func (c *Casino) Bet(username string, amount *big.Int, n int) error {
currentBalance, err := c.getBalance(username)
if err != nil {
    return err
}
amount.Abs(amount)
if currentBalance.Cmp(amount) < 0 {
    return errors.New("insufficient-balance")
}
r := rand.Intn(2023)
if r == n { // correct guess
    reward := new(big.Int).Mul(amount, big.NewInt(2022))
    currentBalance.Add(currentBalance, reward)
    c.setBalance(username, currentBalance)
    fmt.Printf("YOU WIN! Current balance: %d (+%d).\n", currentBalance, reward)
} else {
    currentBalance.Sub(currentBalance, amount)
    c.setBalance(username, currentBalance)
    fmt.Printf("YOU LOSE (%d != %d)! Current balance: %d (-%d).\n", r, n, currentBalance, amount)
}
return nil
}
// ...

• show balance with proof: You give your username to the server and it gives you the balance along with a proofData to prove that you actually own that amount of money.

• example request:

{"Recipient": "Casino", "Command": "ShowBalanceWithProof", "Username": "Orrrrrr"}

• code:

// casino.go
// ...
func (c *Casino) ShowBalanceWithProof(username string) error {
value, proof, err := c.tree.GetWithProof([]byte(username))
if err != nil {
    log.Fatal(err)
}
if value == nil {
    return errors.New("player-not-exist")
}
proofData, err := proof.ToProto().Marshal()
if err != nil {
    log.Fatal(err)
}
fmt.Printf("%d, %s\n", new(big.Int).SetBytes(value), base64.StdEncoding.EncodeToString(proofData))
return nil
}
// ...

• get the flag. In order to retrieve the flag, we need to provide our balance. We also need to provide a proofData, which is generated from the previous section and it's there so that we cannot lie about our balance. The more balance we have, the more bytes of the flag is revealed to us.

• example request:

{"Recipient": "FlagSeller", "Command": "PrintFlag", "Username": "Orrrrrr", "Balance": 674575536530165491749660868130299036066707815144061494924879197906525335081820072153268675251126472982500904339158951753600, "proof_data": [26, 46, 10, 7, 79, 114, 114, 114, 114, 114, 114, 18, 32, 109, 131, 92, 77, 137, 187, 133, 233, 12, 114, 115, 54, 175, 113, 149, 190, 174, 14, 165, 57, 118, 134, 67, 152, 122, 170, 139, 119, 113, 127, 202, 200, 24, 186, 6]}

• code:

// flag_seller.go
// ...
func (fs *FlagSeller) PrintFlag(usename string, balance *big.Int, proofData []byte) error {
var pbProof iavlproto.RangeProof
if err := proto.Unmarshal(proofData, &pbProof); err != nil {
    return fmt.Errorf("bad proof format: %w", err)
}
proof, err := iavl.RangeProofFromProto(&pbProof)
if err != nil {
    return fmt.Errorf("bad proof format: %w", err)
}
if err := proof.Verify(fs.dbRootRetriever()); err != nil {
    return fmt.Errorf("proof verification failed: %w", err)
}
if err := proof.VerifyItem([]byte(usename), balance.Bytes()); err != nil {
    return fmt.Errorf("proof verification failed: %w", err)
}

l := balance.BitLen() / 8
dot3 := "..."
if l >= len(fs.flag) {
    l = len(fs.flag)
    dot3 = ""
}
fmt.Printf("Your flag is: %s%s\n", fs.flag[:l], dot3)
return nil
}
// ...

Analysis

The number of flag bytes revealed to us scales linearly with the number of bytes there are in our balance, so we probably need to have a lot of money to get the full flag. For example, if the flag is $50$ bytes long, we need at least $2^{50*8} = 2^{400}$ coin units to get all of it, which is a really really really big number comparing to our humble $2023$ coins at the beginning.

There are two ways we may want to approach this problem.

The IAVL bug

First one is the IAVL bug. You can see that users' data is stored in the Casino structure, which contains a tree object. This tree data type comes from github.com/cosmos/iavl library.

// casino.go
import (
// ...
	"github.com/cosmos/iavl"
// ...
type Casino struct {
	tree        *iavl.MutableTree
	numAccounts int
}
    
func NewCasino() *Casino {
	tree, err := iavl.NewMutableTree(db.NewMemDB(), 128, true)
	if err != nil {
		log.Fatal(err)
	}
// ...

Upon inspecting the go.mod file, you can see that it uses version v0.19.2, which is nothing surprising until you find out that the real-world IAVL is version v0.19.4 by the time the challenge was released.

// go.mod

module casino

go 1.19

require (
	github.com/cosmos/iavl v0.19.2
	github.com/golang/protobuf v1.5.2
	github.com/tendermint/tm-db v0.6.6
)

So, I began searching for clues, like "iavl v0.19.2 attack", "cosmos iavl v0.19.2 tree vulnerability attack", then I came upon this blog:

which was suspicious, because it released around the time of v0.19.3 according to this change log. " Pass IAVL Proof Verification?" Maybe there's some way we can craft a fake proofData to send to the PrintFlag function for any balance we wish to? Anyways, reading through the blog (not the one I screenshot-ed above, this one, dunno why it's not in Google search anymore 😕 that one's just for showcase that we tried to find stuffs), it seems like whatever bug they found, it was really bad. So I thought to myself: This must be it.

Then I noticed the change in v0.19.3, it seems like the change in the newer version suggests something about the attack we should come up with :)

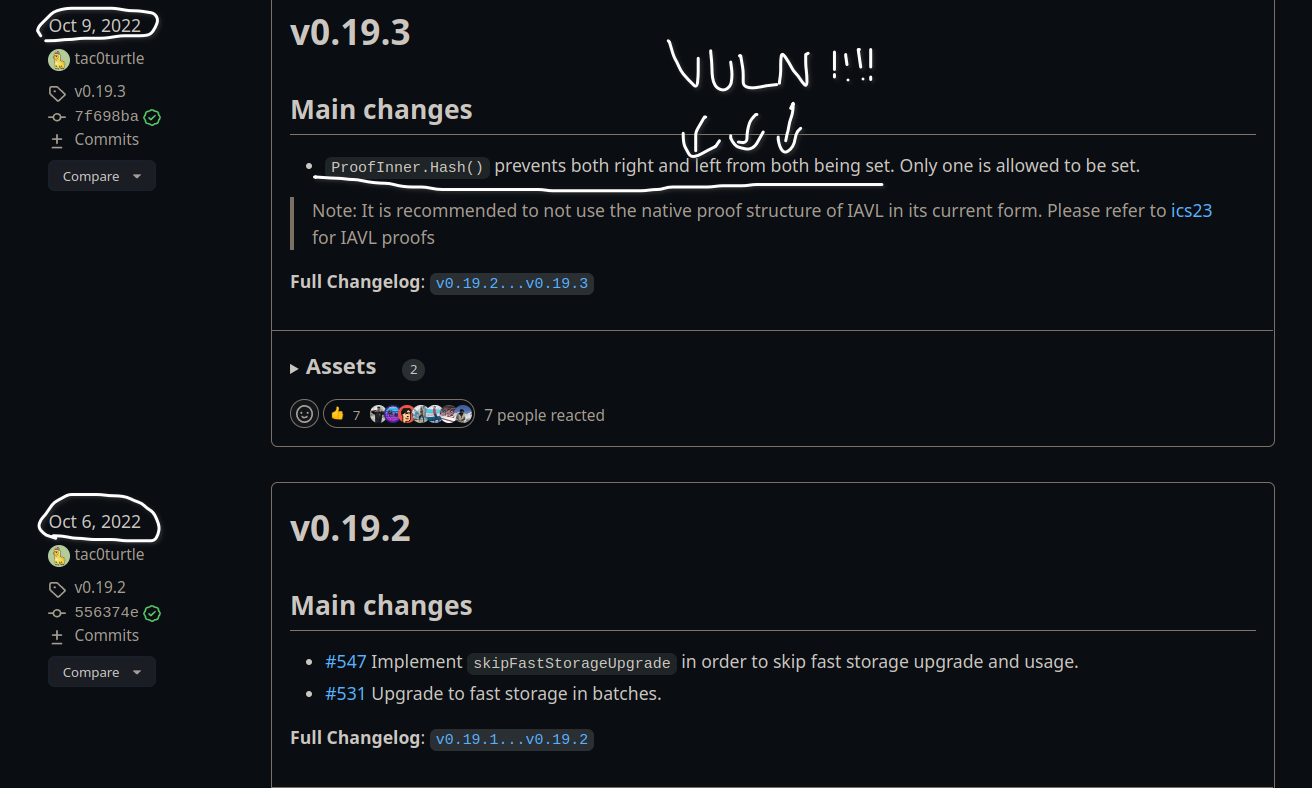
However, our investigation about the tree stuff ends here, because this is where me and my teammate stopped (you know why 🙂); and also this blog's about attacking the Go's rand stuff 😗 If you want to read more about the IAVL bug, you should visit these two links, provided by a fellow Discord member:

• Binance Chain Bridge Exploitation Writeup - Part 1
• Binance Chain Bridge Exploitation Writeup - Part 2

The Go math/rand stuff

The second way you could dig at this challenge is by exploiting the rand.Intn(n) function from math/rand library. Remember, the server creates random numbers in $[0, 2023)$ and you can try to guess them in order to gain/or lose money.

We can try to go all random; however, that only guarantees us to get the correct answer in a probability of $\frac{1}{2023}$, and from the way the server rewards us, +$2022$ * balance for winning and -balance for losing, it seems like we will just be stuck in the same loop forever if we do that.

---

If only somehow you can find a hidden pattern in the way the server generates the numbers, which is just this line of code btw :333

r := rand.Intn(2023)

then you can use it to predict future values, keep winning and rocketing yourself to your target balance. And from the title, you already know that it is possible.

The reason this is feasible because the math/rand library "implements pseudo-random number generators" which is "unsuitable for security-sensitive work" according to this link. It also states that "This package's outputs might be easily predictable regardless of how it's seeded." Great! But how predictable is it?

---

A pseudo-random number generator, or PRNG, like this would generate all of their supposed random numbers based on a seed value. If you know the seed, you basically become god and predict all n values in the bet game.

As some players have pointed out, it is possible to recover the seed of Go's PRNG, because:

This means we just need to brute-force every value from $0$ to $2^{32} - 1 = 4294967295$, for which, in today's computer standards, can be done within an hour or so in a low-end laptop, 20 minutes if running multiple cores. For every seed, we set seed by rand.Seed(seed) then call rand.Intn(2023) a few times and compare the outputs with the server's n(s), which can be obtained for free by keep betting $0$ coins. When we've found and verified the seed, we just need to keep betting with our balance with n = rand.Intn(2023) to get the flag.

While it is very simple to setup the code to do this, an hour, to me, still feels like it's too much. If you code wrong (probably you won't but who knows?), you would've to spend another hour to debug 🙂 Luckily tho, we can find the pattern of rand.Intn(2023) without the seed 😉, thus solving this challenge in a matter of seconds.

Finding pattern in rand.Intn(n)

Graphing the Calls

r := rand.Intn(2023)

Staring at a single line of code won't help a thing. So I decided to use the power of ctrl-click-into-a-function-because-it-helps-us-going-back-to-its-definition-and-i-hope-i-could-have-a-better-name-for-this in VSCode and dive into the code hierarchy and here is the progress:

---

As you can see, we've got pretty much everything up until the Int63() function. To look at the code for that, we need to go to rng.go, which is at the same directory as rand.go (the reason I got this is because my friend found the code for Int63() at https://go.dev/src/math/rand/rng.go, and I was like wait aren't we also have this file in the system too?), and we've got the complete picture:

---

While the above graph looks kinda crazy (or not, idk...), when we create an abstract map for them, it is actually surprisingly simple if we just focus on the case where n = 2023 or n is a relatively small number to $2^{31}$ in general.

Formualize it

The graph above can be simplified as a formula in Python:

rand.Intn(n) == ((rand.Uint64() & ((1<<63) - 1)) >> 32) % n  # n is small

Because taking the last $63$ bits then shift $32$ bits to the right is equivalent to shift $32$ bit to the right and taking the last 31 bits, we can rewrite it like this:

rand.Intn(n) == ((rand.Uint64() >> 32) & ((1<<31) - 1)) % n	 # n is small

we can see that & ((1<<31) - 1)) is just % (2**31), so:

rand.Intn(n) == (rand.Uint64() >> 32) % (2**31) % n			 # n is small

This implies if we have two Go programs set to the same seed, one outputting 1 number from rand.Intn(n) and the other outputting 1 number from rand.Uint64(), then the above equation holds.

---

... You're probably wondering why I keep mentioning n is small in the code comment. Well, the above statement is not entirely true. It only happens in high probability for small n. For big n $< 2^{31}$, rand.Intn(n) may call rand.Uint64() multiple times before outputting a number. If we investigate into the rand.Int31n(n) function,

func (r *Rand) Int31n(n int32) int32 {
	// ...
	max := int32((1 << 31) - 1 - (1<<31)%uint32(n))
	v := r.Int31()
	for v > max {
		v = r.Int31()
	}
	return v % n
}

you can see that there also exists a max variable, and we have to call rand.Int31() repeatedly until we hit a value <= max. If n is small, max would be very close to $2^{31}$, thus we most likely just need to call rand.Int31() only once for each rand.Intn(n).

Oh, but there is an exception if n is a power of $2$. If n is $2^{\text{something}}$, every call to rand.Intn(n) will definitely call rand.Int31() once.

// Int31n returns, as an int32, a non-negative pseudo-random number in the half-open interval [0,n).
// It panics if n <= 0.
func (r *Rand) Int31n(n int32) int32 {
	// ...
	if n&(n-1) == 0 { // n is power of two, can mask
		return r.Int31() & (n - 1)
	}
    // ...

More Pattern

Consider $R$ a list of consecutive outputs from rand.Intn(n), $S$ a list of consecutive outputs from rand.Uint64() setting to the same seed starting at the same time, when n is a small number $< 2^{31}$, we most likely have:

where $S_i, R_i$ is the $i$-th output of rand.Uint64() and rand.Intn(n).

What's great about this formula is that we can now derive a pattern for rand.Intn(n) through the pattern of rand.Uint64(). And it turns out the pattern of rand.Uint64() is very simple. When you look at the code for rand.Uint64(), you can see it get output from rng.vec array while updating it.

// /usr/lib/go-1.18/src/math/rand/rng.go
const (
	rngLen   = 607
	rngTap   = 273
	rngMax   = 1 << 63
	rngMask  = rngMax - 1
	int32max = (1 << 31) - 1
)

// ...
type rngSource struct {
	tap  int           // index into vec
	feed int           // index into vec
	vec  [rngLen]int64 // current feedback register
}

// ...

// Seed uses the provided seed value to initialize the generator to a deterministic state.
func (rng *rngSource) Seed(seed int64) {
	rng.tap = 0
	rng.feed = rngLen - rngTap
// ...

// Uint64 returns a non-negative pseudo-random 64-bit integer as an uint64.
func (rng *rngSource) Uint64() uint64 {
	rng.tap--
	if rng.tap < 0 {
		rng.tap += rngLen
	}

	rng.feed--
	if rng.feed < 0 {
		rng.feed += rngLen
	}

	x := rng.vec[rng.feed] + rng.vec[rng.tap]
	rng.vec[rng.feed] = x
	return uint64(x)
}

You don't need to know how the rng.vec is created to figure out a pattern for rand.Uint64(). Here, you just need to consider it to be a bunch of random numbers. The important thing you'll need to care is that rng.vec:

• only uses the numbers in it to update itself.

• the way it creates new number from older ones.

If you're familiar with the structure of LFSR, or Linear Feedback Shift Register, you would probably recognize this is kinda like that. The terms like tap and feed make more sense, and you can deduce the following relationship between some of the $S_i$(s):

(while it is seemingly enough to conclude $S_i = S_{i-607} + S_{i-273}$ based on the x := rng.vec[rng.feed] + rng.vec[rng.tap] line, however since rng.vec is stored in an int64 array, we have to include the$\mod 2^{64}$ in there.)

The tale of adding two numbers

(i think this section is kinda overkill, but whatever -_-)

What happens to the result when we add two $b$-bit numbers $A$ and $B$? Well, sometimes, the $A+B$ fits into a $b$-bit value. In this case,

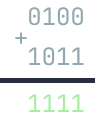
The other times, the result overflows, at most 1 bit into the left. In this case,

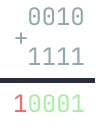
What is also interesting when we add two numbers, is that if you ignore some of $m$-lower bits at the end, the addition in the higher bits is still true in some cases. This is essentially saying that,

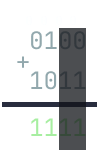
However, sometimes, since the addition in the lower $m$-bits results in a carry, we will also get this case:

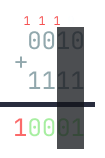
Piecing the puzzle together

(i'm not sure if this reasoning is correct... but I'll try my best)

(at first I was going to use the figures similar to the previous section but I don't know how, so I just stick with the formula, hope this make senses to all of you 🙂)

You're probably know where this is going. Because:

... we have:

(i dunno if the notation $+ \{a, b\}$ actually represents add $a$ or $b$ or not... But that's what I meant :))

... shift right both sides by $32$...

... and we reduce both sides$\mod 2^{31}$...

($\{0, 2^{32}\}$ vanishes cuz $0$ or $2^{32}$ equals $0$ mod $2^{31}$)

But this also means:

Now the final ingredient, taking$\mod n$ on both sides, and voilà!:

Take your balance to the infinity and beyond 🚀

Now we've known how the outputs of rand.Intn(n) are related. We can collect numbers generated by the server into a list $R$ by just betting random numbers in $[0, 2023)$. You can bet $0$ coin units to prevent yourself from losing money.

After $607$ numbers are collected, you choose from one of the 4 possibilities that states either the next output $R_i$ is:

and bet $R_i$ with that guess.

Because win amount is $2022$ times bigger than lose amount, while our possibility of hitting the correct answer is $\frac{1}{4}$, our money will be increasing in the long run. If we bet with some amount that is proportional to balance like balance/2, this allows our money to grow exponentially, makes it easy to hit some crazy big number like $2^{400}$ in no time.

(i'm not sure that's optimal or not... but balance/2 works so I don't think too much about that 🙂)

When you get $2^{400}$ coin units, you request showBalanceWithProof to get proofData then submit it along with your balance to PrintFlag to grab some flag! (yey)

Appendices

Solve script

from   tqdm     import trange
from   pwn      import remote
from   sage.all import *
import base64
import json

host = '192.53.115.129'
port = int(31339)

########## Connect ###########
io = remote(host, port)
# io = process(['./src/casino'])

def request(data):
    if isinstance(data, str):
        data = data.encode()
    elif not isinstance(data, bytes):
        data = str(data).encode()
    io.send_raw(data + b'\n')

def recvline():
    return io.recvline().strip().decode()

def get(data):
    request(json.dumps(data))
    return recvline()

########### Requests #############

def register(username):
    return get({
                "Recipient": "Casino",
                "Command": "Register",
                "Username": username
            })

def bet(username, amount, number):
    answer = get({
        "Recipient": "Casino",
        "Command": "Bet",
        "Username": username,
        "Amount": amount,
        "N": number
    })

    serverGuess = int(answer.split(' ')[2][1:]) if 'YOU WIN' not in answer else number
    ourBalance  = int(answer.split(' ')[-2])

    return serverGuess, ourBalance

def showBalance(username):
    answer = get({
        "Recipient": "Casino",
        "Command": "ShowBalanceWithProof",
        "Username": username
    })

    ourBalance = int(answer.split(' ')[0][:-1])
    proofBytes = base64.b64decode(answer.split(' ')[1])
    return ourBalance, proofBytes

def printFlag(username, balance, proof):
    return get({
                "Recipient": "FlagSeller",
                "Command": "PrintFlag",
                "Username": username,
                "Balance": balance,
                "proof_data": list(proof)
            })
    
########### Main #############

USER = 'mistsu'
register(USER)

print(f'[i] Collecting server outputs...')
serverOutputs = []
for i in trange(607):
    serverOutput, balance = bet(USER, 0, 0)
    serverOutputs.append(serverOutput)

print(f'[i] Guessing server\'s outputs with probability of 1/4...')
i = 607
while balance < 2**(50*8):
    ourGuess = (serverOutputs[i - 607] + serverOutputs[i - 273]) % 2023
    serverOutput, balance = bet(USER, balance//2, ourGuess)
    serverOutputs.append(serverOutput)

    print(f'[i] Server actual output: {serverOutput}')
    print(f'[i] Our output:           {ourGuess}')
    print(f'[i] Balance:              {balance}')
    print(f'---------------------------------------------------')

    i += 1

ourBalance, proofBytes = showBalance(USER)
print(printFlag(USER, ourBalance, proofBytes))

Modifying dockerfile

Yeah, building a docker for this challenge sucks, because it keeps yelling at us that there's no go.sum file :< So we decided to fix the Dockerfile, add a compose.yml file so that we can just docker compose it, making our lives easier 🙂 . Here are them 2 files:

Dockerfile (modified)

FROM golang:1.19-alpine

RUN apk add socat

RUN addgroup -S casino && adduser -S casino -G casino
USER casino:casino
WORKDIR /home/casino

# Create go.mod file
COPY ./go.mod .
RUN go mod download

# This is just for a reminder to put a flag file in here :)
COPY ./flag .  

# Copy everything else and build binary.
COPY . .
RUN go get casino 
RUN mkdir ./build
RUN go build -o ./build/casino

EXPOSE 31339

CMD socat -T 30 -d -d TCP-LISTEN:31339,reuseaddr,fork EXEC:"./build/casino"

compose.yml

services:
    casino2:
        build: .
        ports:
            - "31339:31339"

After starting the container, you can connect to localhost:31339 to play the challenge 😗