Introduction

This is a crazy challenge that drained my team's brains 😢 and we couldn't solve it in time of the CTF 🙁 After 2 days of trying to brainstorm, we have finally be able to crack the code, with a little bit of luck 😗

Since the intended solution will be provided by the author catto after the finals (18/12), which is over ONE MONTH AFTER from when I'm writing these lines (why it gotta take so long catto 😭 😭 😭), I decided to create my own writeup to explain our method of solving this problem 😗

Challenge

Description

The server generates a securely random 64-bit hex string password that is kept secret. We as the clients have to guess the secret password to get the flag.

The server gives us hints about the password through the output of the encrypt(password), which is a function we can call as many times as we can, each time it seemingly produces a different output despite feeding the same input to the function.

This writeup provides a way to obtain the flag with 8 outputs of encrypt(password) in a probability of about $1/40$.

Code

#!/usr/bin/env python3
from secret import SECRET_BASIS
from secrets import token_hex
import random
import os
import copy

assert len(SECRET_BASIS) == len(SECRET_BASIS[0]) == 128
BASIS = copy.deepcopy(SECRET_BASIS)

def f(M: list[list[int]], C: list[int]) -> list[int]:
    v = [0] * len(M[0])
    for c, m in zip(C, M):
        if c:
            v = [x ^ y for x, y in zip(v, m)]
    return v

def random_bits(n: int) -> list[int]:
    return list(map(int, bin(random.getrandbits(n))[2:].rjust(n, "0")))

def encrypt(message: bytes) -> str:
    global BASIS
    random.shuffle(BASIS)
    M = [b for c in message for b in map(int, "{:08b}".format(c))]
    ct = []
    for bit in M:
        C = random_bits(64)
        v = f(BASIS[:64], C) if bit else f(BASIS[64:], C)
        ct.extend(v)
    ct = "".join(map(str, ct))
    return bytes([int(ct[i:i+8], 2) for i in range(0, len(ct), 8)]).hex()

def decrypt(ciphertext: str) -> bytes:
    # TODO: implement this pls
    pass

def action_prompt() -> int:
    print('''============= MENU =============
    1. Have a guess
    2. Get ciphertext
    3. Change password
    4. Quit
================================\n''')
    try:
        option = int(input("Your option> "))
    except:
        return None
    return option

def chall():
    try:
        password = token_hex(8)
        while True:
            option = action_prompt()
            if option == 1:
                user_password = input("Input your password (hex): ")
                if user_password == password:
                    print(f"Is taking the red pill worth it? Here is the truth that you want: {os.environ['FLAG']}.")
                else:
                    print("Guess you can't escape the matrix after all.")
                break
            elif option == 2:
                print(f"Leaky ciphertext: {encrypt(bytes.fromhex(password))}")
            elif option == 3:
                print("Generating super secure password ...")
                password = token_hex(8)
            elif option == 4:
                print("Maybe the truth is not that important, huh?")
                break
            else:
                print("Invalid option.")
            print("\n")
    except:
        print("An error occured!")

chall()

Analyzing stuffs...

Let's first dissect everything in the source code to see what it does and how to make sense of the data given to us 😗 If you've already known what to expect, you can hop onto the next section to see the discussion of the solution ❤️

encrypt(message) converts message in hex form to its binary form M as a list of 0 and 1s,

def encrypt(message: bytes) -> str:
    ...
	M = [b for c in message for b in map(int, "{:08b}".format(c))]
    ...

For each bit of M, it generates a random 64-bit value C (also a list of 0 and 1s),

def random_bits(n: int) -> list[int]:
    return list(map(int, bin(random.getrandbits(n))[2:].rjust(n, "0")))
	
def encrypt(message: bytes) -> str:
    ...
    for bit in M:
        C = random_bits(64)
        ...

calls f(C, [:64]) or f(C, BASIS[64:]) depending on the current bit of M, appends the result of the call to the ct variable.

def encrypt(message: bytes) -> str:
    global BASIS
	...
    ct = []
    for bit in M:
        C = random_bits(64)
        ct = []
        for bit in M:
            C = random_bits(64)
            v = f(BASIS[:64], C) if bit else f(BASIS[64:], C)
            ct.extend(v)

BASIS is a global variable, a 2-dimensional list with size 128x128 with unknown content whose rows are shuffled in every call to encrypt().

assert len(SECRET_BASIS) == len(SECRET_BASIS[0]) == 128
BASIS = copy.deepcopy(SECRET_BASIS)

...
def encrypt(message: bytes) -> str:
    global BASIS
    random.shuffle(BASIS)
    ...

After loop, ct is then converted to its hex form and returned to the user. From this code, it is safe to assume that the value of ct is a list consisting of all 0s and 1s.

def encrypt(message: bytes) -> str:
    ...
    ct = []
    for bit in M:
        ...
        ct.extend(v)
	ct = "".join(map(str, ct))
    return bytes([int(ct[i:i+8], 2) for i in range(0, len(ct), 8)]).hex()

Also, it can be deduced from ct and the type hints and operations of f(), which is just bunch of repeated XORs of values in v andM[i] (M is BASIS[:64] or BASIS[64:]), that BASIS also consists of 128x128 values of 0s and 1s.

def f(M: list[list[int]], C: list[int]) -> list[int]:
    v = [0] * len(M[0])
    for c, m in zip(C, M):
        if c:
            v = [x ^ y for x, y in zip(v, m)]
    return v

All of these XORs and 2-dimensional arrays and lists of 0s and 1s seem to point everything into viewing those things as addition of matrices and vectors in $GF(2)$. And it turns out we can view:

• BASIS as a 128x128 matrix in $GF(2)$.

• As for f(M, C) , there are two ways to view this function:

  You can either view it as an operation that produces a 1xn vector v by multipling a 1xm vector C with an mxn matrix M,

  $$\overrightarrow{v} = \overrightarrow{C} * M$$

  or as an operation that generates a linear combination of the rows in M with coefficients on C.

  $$\begin{matrix} \overrightarrow{v} = \sum_{i=0}^{m} {C_i}\overrightarrow{{M_i}} & & C_i \in \{0, 1\} \end{matrix}$$

  I'll choose to see it in the 2nd way because it helps when discussing the solution later 😁

• encrypt(message) randomizes C and uses f(BASIS[...], C) to produce random linear combinations of the first 64 rows of BASIS or the last 64 rows of BASIS depending on the current looping bit of M or message (0 - first 64, 1 - last 64). All of the resulting vectors are stored in ct before converted into hex form and returned to the user.

• ct is a list of 64 different 128-dimensional vectors $\overrightarrow{v_i}$ in $GF(2)$ that is either spanned by the last 64 rows of BASIS or the first 64 rows of BASIS. Each vector in ct corresponds to a bit in password.

Now we know how to view the encrypted password, let's discuss the solution!

How to know the bits of password?

In order to get all the bits of password, we must be able to classify which vector $\overrightarrow{v_i}$ in ct belongs to which vector space. Is $\overrightarrow{v_i}$ generated from BASIS[:64] (so $password_{i}$ is 0), or BASIS[64:] (so $password_{i}$ is 1)?

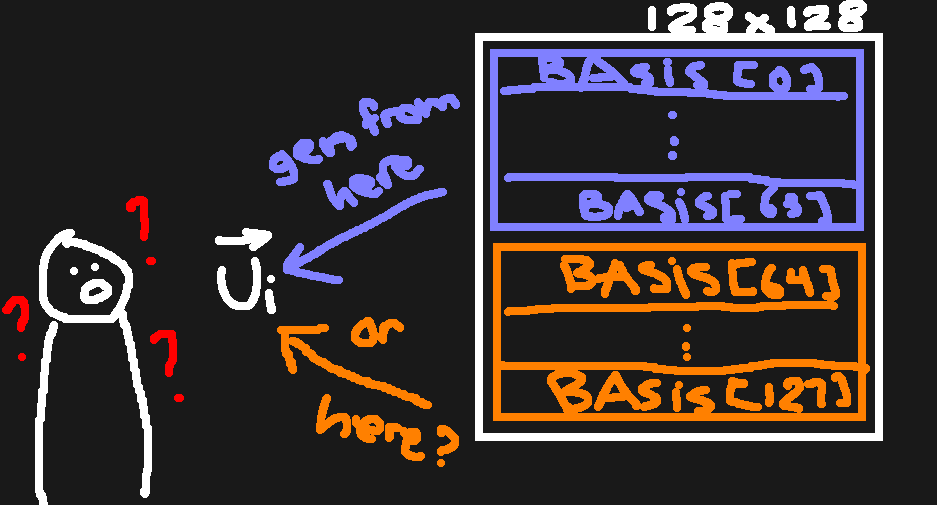
We don't even have BASIS, so if we know a particular vector is formed by a set of 64 rows in BASIS, we can't even tell if that set positions at the top of the matrix or the bottom! The only bet for us is to know which bit is different from which bit by comparing the vector space that spans the corresponding vectors. If we've got the mapping of which bit is different from which bit, we can set one random bit to be 0 and let the mapping does the rest. This gives us the probability of finding the correct answer at $1/2$ (given the mapping, of course 😃)

Notations

Before moving on, I think I should introduce some notations here to help discussing the next part.

• Bit i of password is $password_i$.

• $\overrightarrow{v_{i, a}}$ is the i-th vector of ct, generated at a-th time we request to get encrypt(password).

• $S_{i, a}$ be the set of rows in BASIS that generates $\overrightarrow{v_{i, a}}$.

  Based on the rule of this challenge, we can see that in an $a$-th encrypt operation:

  • $S_{i, a} =$ BASIS[:64] when $password_i = 0$,
  • $S_{i, a} =$ BASIS[64:] when $password_i = 1$,

  Which leads to these properties:

  • $S_{i, a} = S_{j, a}$ when $password_i = password_j$.
  • $S_{i, a} \neq S_{j, a}$ when $password_i \neq password_j$.

• $P(e)$ is the probability of some event $e$ happening.

• $\#S$ is the length of set $S$.

Matrix1.0

In Glitch in the matrix 1.0, comparing $password_i$ and $password_j$ is very much doable. To solve this challenge, we have to provide a way to differentiate between the vectors that are either generated from BASIS[:64] or BASIS[64:].

Because password doesn't change every-time we call encrypt and most importantly, BASIS is not changed in the entire runtime of the program, $\overrightarrow{v_{i, a}}$ is generated from the same set of 64 vectors as $\overrightarrow{v_{i, b}}$ for any $a, b$, or $S_{i, a} = S_{i, b}.$

This means that we can request 64 encrypts to obtain $\overrightarrow{v_{i, 0}}, \overrightarrow{v_{i, 1}}, \overrightarrow{v_{i, 2}}, ..., \overrightarrow{v_{i, 63}}$ that is in the same vector space as BASIS[:64] or BASIS[64:]. In order to verify if $password_{i} = password_{j}$, or $S_{i, a} = S_{j, a}$, I created a 128x128 matrix that looks like this:

If the rank of this matrix is $64$, $\overrightarrow{v_{i, 0}}, \overrightarrow{v_{i, 1}}, \overrightarrow{v_{i, 2}}, ..., \overrightarrow{v_{i, 63}}, \overrightarrow{v_{j, 0}}, \overrightarrow{v_{j, 1}}, \overrightarrow{v_{j, 2}}, ..., \overrightarrow{v_{j, 63}}$ comes from the same span of 64 vectors, so $S_{i, a} = S_{j, a}$, and we can conclude that $password_i = password_j$. If the rank of this matrix is $128$, the opposite is true and we get $password_i \neq password_j$.

In script, we fix $i = 0$ and let $j$ runs from $1 - 63$ to generate the mapping and recover the password with probability of $1/2$.

Matrix2.0

Glitch in the matrix 2.0 is the updated version where BASIS is shuffled every-time we request a new encrypt(password). This means that the property that:

$\overrightarrow{v_{i, a}}$ is generated from the same set of 64 vectors as $\overrightarrow{v_{i, b}}$ where $a \neq b$, or $S_{i, a} = S_{i, b}$,

is not correct this time around, which is very sad 😭. We also cannot refer to BASIS[:64] and BASIS[64:] as constants anymore.

Probability hint

After a while, a hint came out from the author:

And we still had no idea what the hell she is talking about until the end of the CTF 😦

...

And then, a thought comes to my mind:

While it's true that $\overrightarrow{v_{i, a}}$ is not gonna be generated from the same set of 64 vectors as $\overrightarrow{v_{i, b}}$ if $a \neq b$, some of the vectors in those sets might overlap. Let $P(S_{i, a} \cap S_{i, b} = \{\})$ be the probability of $S_{i, b}$ purposefully choosing a set of different 64 vectors to $S_{i, a}$ in a list of 128 vectors, then:

proving that this is a very, very, very, very, very unlikely event.

This gives me an insight that the sets $S_{i, a}$ and $S_{i, b}$ almost always overlap, and from above we've got:

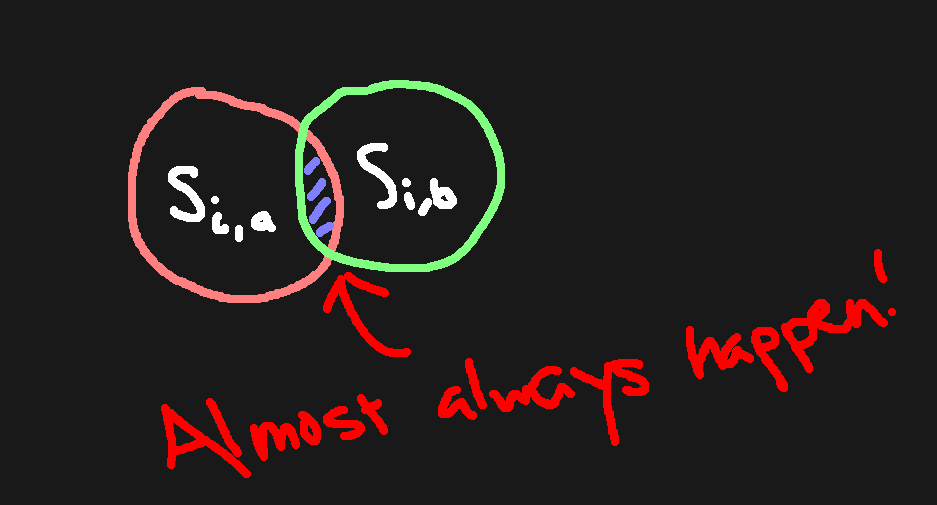
This might be the "probability" thing catto was talking about! Also from this another idea is formed!

Detecting $\lfloor{\frac{128}{n}}\rfloor + 1$ similar bits in password

Let's say we generate encrypt(password) $n$ times for $n \ge 3$.

And somehow, for a certain value of $password_i$, we obtain the vectors $\overrightarrow{v_{i, 0}}, \overrightarrow{v_{i, 1}}, ..., \overrightarrow{v_{i, n-1}}$ such that:

This means that $S_{i, 0} \cup S_{i, 1} \cup S_{i, 2} \text{ } \cup \text{ } ... \text{ } \cup S_{i, n-1}$ contains about 127 rows in BASIS except one/some row(s). The remaining row(s) of BASIS would be present in the set of $S_{j, 0} \cup S_{j, 1} \cup S_{j, 2} \text{ } \cup \text{ } ... \text{ } \cup S_{j, n-1}$ where $password_j \ne password_i$ as $S_{j, a}$ always contains the vectors that $S_{i, a}$ doesn't have.

And somehow, we can find a set of $\lfloor{\frac{128}{n}}\rfloor + 1$ elements $\{password_{i_0}, password_{i_1}, ..., password_{i_{\lfloor{\frac{128}{n}}\rfloor}}\}$, where $password_{i_0} = password_{i_1} = \text{ } ... = password_{i_{\lfloor{\frac{128}{n}}\rfloor}}$.

So, this matrix $M$, which has $n(\lfloor{\frac{128}{n}}\rfloor + 1) > 128$ rows,

must have rank $\le 127$ as all of these vectors are generated from the set of $S_{i, 0} \cup S_{i, 1} \cup S_{i, 2} \text{ } \cup \text{ } ... \text{ } \cup S_{i, n-1}$, which contains only $\le 127$ rows of BASIS.

If we change just one of $password_{i_k}$ to a different bit from the rest, the above matrix $M$ will most likely have higher rank (often $128$) than before, since there will be a row in $M$ that is a linear combination of the vectors including the one(s) that is/are not in $S_{i, 0} \cup S_{i, 1} \cup S_{i, 2} \text{ } \cup \text{ } ... \text{ } \cup S_{i, n-1}$.

Here comes our mechanism to detect $\lfloor{\frac{128}{n}}\rfloor + 1$ similar bits in password. In particular, if we randomize $\{{i_0}, {i_1}, ..., {i_{\lfloor{\frac{128}{n}}\rfloor}}\}$ enough times and construct $M$, we might stumble across a situation where $M$ has rank $\le 127$ and we can use this to say that $password_{i_0} = password_{i_1} = \text{ } ... = password_{i_{\lfloor{\frac{128}{n}}\rfloor}}$ with high probability.

However, in order for this to work, we need to make sure to choose $n$ so that both of these conditions hold:

1. $\#(S_{i, 0} \cup S_{i, 1} \cup S_{i, 2} \text{ } \cup \text{ } ... \text{ } \cup S_{i, n-1}) \le 127$ occurs in high probability.

2. Choose $\{{i_0}, {i_1}, ..., {i_{\lfloor{\frac{128}{n}}\rfloor}}\}$ that $password_{i_0} = password_{i_1} = \text{ } ... = password_{i_{\lfloor{\frac{128}{n}}\rfloor}} = 0$ in high probability.

It turns out, if scenario 1. occurs more likely, scenario 2. will occur less likely and vice versa, so we need to balance $n$. Through trials and errors, I've decided to choose $n = 8$ and the correct set $\{{i_0}, {i_1}, ..., {i_{\lfloor{\frac{128}{n}}\rfloor}}\}$ is found in a probability of about $1/20$, after brute forcing at most $400000$ sets.

Recover the remaining bits in password

Remember the matrix $M$ from the last section? We can use it to detect the rest of the bits in password. For every $j$-th bit in password that $j \notin \{{i_0}, {i_1}, ..., {i_{\lfloor{\frac{128}{n}}\rfloor}}\}$, I decided to construct a new matrix $N$ from $M$ that is:

Then compares $rank(N)$:

• $= rank(M)$, we have $password_j = password_{i_0} = password_{i_1} = \text{ } ... = password_{i_{\lfloor{\frac{128}{n}}\rfloor}}$.

• $> rank(M)$, we have $password_j \neq password_{i_0} = password_{i_1} = \text{ } ... = password_{i_{\lfloor{\frac{128}{n}}\rfloor}}$.

With this information, we can recover password with a probability of $1/2$.

Solve code

This piece of code implements what I've just described above, with some small changes:

• Constructs $M$ by brute-forcing through a bigger random list, $\{{i_0}, {i_1}, ..., {i_{\lfloor{\frac{128}{n}}\rfloor + 1}}\}$ instead of just $\{{i_0}, {i_1}, ..., {i_{\lfloor{\frac{128}{n}}\rfloor}}\}$. This allows $M$ to have even more rows, ensuring us that we get $M$ where $rank(M) \le 127$ actually because of $\#(S_{i, 0} \cup S_{i, 1} \cup S_{i, 2} \text{ } \cup \text{ } ... \text{ } \cup S_{i, n-1}) \le 127$, not just some false positives.

• Uses multiprocessing to find the list $\{{i_0}, {i_1}, ..., {i_{\lfloor{\frac{128}{n}}\rfloor + 1}}\}$ that yields $rank(M) \le 127$ faster.

from   Crypto.Util.number       import *
from   tqdm                     import tqdm, trange
from   pwn                      import remote, process
from   sage.all                 import *
from   multiprocessing          import Process, Queue
import random, time

host = '34.132.73.130'
port = int(8003)

B = 64
N = 128
K = 8
targetRank = N-1
def convertToMatrix(input: bytes):
    bits = ''
    for byte in input:
        bits += f'{byte:08b}'
    bits = list(map(int, bits))
    bits = [bits[i:i+128] for i in range(0, len(bits), 128)]
    return Matrix(GF(2), bits)


class Solver:
    # -------------------------------------- CONNECT --------------------------------------
    def __init__(self) -> None:
        self.io = remote(host, port)

    def __del__(self):
        self.io.close()

    def request(self, data):
        if isinstance(data, str):
            data = data.encode()
        elif not isinstance(data, bytes):
            data = str(data).encode()
        self.io.send_raw(data + b'\n')

    def recvline(self):
        return self.io.recvline().strip().decode()

    # -------------------------------------- REQUEST --------------------------------------
    def get(self, option):
        self.io.recvuntil(b'option> ')
        self.request(option)

    def encrypt(self):
        self.get(2)
        return convertToMatrix(bytes.fromhex(self.recvline().split(': ')[-1]))

    def submit(self, key):
        self.get(1)
        self.request(key)

    def changePassword(self):
        self.get(3)

    # -------------------------------------- MAIN --------------------------------------
    def execOneCore(self, U, Ntries, delta, retQueue, progBar):
        choices = list(range(1, B))
        for _ in range(Ntries):
            random.shuffle(choices)
            combination = choices[:N//K + int(N%K != 0) + delta]
            
            P = block_matrix(
                    [[U[i]] for i in combination]
                )
            
            if P.rank() <= targetRank:
                retQueue.put([
                    P.rank(), combination
                ])
                break

            if not retQueue.empty():
                break

            progBar.update()

    def findBestComb(self, U, ncores=4, Ntries=100000, delta=2):
        # Progress bars
        progBars = []
        for i in range(ncores):
            progBar = tqdm(desc=f'#{i}', total=Ntries)
            progBars.append(progBar)

        # Hold return values of all cores
        retQueue = Queue()
        
        # Create new processes
        futures = []
        for _ in range(ncores):
            futures.append(Process(
                            target=self.execOneCore,
                            args=(
                                U, Ntries, delta,
                                retQueue, 
                                progBars[_], 
                            )))

        # Start all processes
        for future in futures:
            future.start()

        # Wait for all process to finish :)
        for future in futures:
            future.join()

        # Close all progress bars
        for progBar in progBars:
            progBar.close()

        # Get answer!
        if not retQueue.empty():
            rank, comb = retQueue.get()
            return rank, comb
        
        return None, None

    def main(self):
        M = []
        for i in range(K):
            M.append(self.encrypt())

        U = []
        for i in range(B):
            u = []
            for j in range(K):
                u.append([M[j][i, :]])
            U.append(block_matrix(u))

        print(f"[i] Find combination of vectors that forms a matrix with rank <= {targetRank}...")
        rank, comb = self.findBestComb(U, Ntries=100000, delta=2)
        if comb == None:
            return False
        print(f"[i] Best rank: {rank}")
        print(f"[i] Best combination: {comb}")
        # print(f"[i] Debug matrix:\n{block_matrix([[U[i]] for i in comb], subdivide=False)}")

        # Deduce the password bits...
        passwordbits = ''
        for j in range(B):
            if j in comb:
                passwordbits += '0'
                continue

            P = block_matrix(
                [[U[i]] for i in comb + [j]]
            )

            if P.rank() > rank:
                passwordbits += '1'
            else:
                passwordbits += '0'

        # Convert it to hex and send to server :)
        password = bytes([int(passwordbits[i:i+8], 2) for i in range(0, len(passwordbits), 8)]).hex()
        self.submit(password)
        print('[i] Password is (maybe):', password)
        print('[i] Password bits are (maybe):', passwordbits)
        
        # Get answer from server, which is estimated to be successful at around 1/20...
        answer = self.recvline()
        print('server>', answer)
        if 'Here is the truth that you want' in answer:
            return True
        return False

cnt = 0
while True:
    cnt += 1
    solver = Solver()
    if solver.main():
        break
print(f"[i] Solver took {cnt} times.")